-
Notifications
You must be signed in to change notification settings - Fork 41
/
Copy pathanalyse-des-correspondances-multiples.Rmd
623 lines (484 loc) · 25.3 KB
/
analyse-des-correspondances-multiples.Rmd
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
558
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
---
title: "Analyse des correspondances multiples (ACM)"
---
```{r options_communes, include=FALSE, cache=FALSE}
source("options_communes.R")
```
<div class="guide-R">
Une version actualisée de ce chapitre est disponible sur **guide-R** : [Analyse factorielle](https://larmarange.github.io/guide-R/analyses_avancees/analyse-factorielle.html)
</div>
<div class="webin-R">
Ce chapitre est évoqué dans le webin-R #11 (Analyse des Correspondances Multiples sur [YouTube](https://youtu.be/fIZblrfenz0).
</div>
Il existe plusieurs techniques d'<dfn>analyse factorielle</dfn><dfn data-index="factorielle, analyse"></dfn> dont
les plus courantes sont l'<dfn>analyse en composante principale</dfn> (<dfn>ACP</dfn>) portant sur des
<dfn data-index="variable quantitative">variables quantitatives</dfn><dfn data-index="quantitative, variable"></dfn>,
l'<dfn>analyse factorielle des correspondances</dfn><dfn data-index="correspondances, analyse factorielle"></dfn>
(<dfn>AFC</dfn>) portant sur deux
<dfn data-index="variable qualitative">variables qualitatives</dfn><dfn data-index="qualitative, variable"></dfn>
et l'<dfn>analyse des correspondances multiples</dfn> (<dfn>ACM</dfn>) portant
sur plusieurs variables qualitatives (il s'agit d'une extension de l'AFC).
Pour combiner des variables à la fois quantitatives
et qualitatives, on pourra avoir recours à l'<dfn>analyse factorielle avec données mixtes</dfn><dfn data-index="mixtes, analyse factorielle avec données"></dfn>.
Bien que ces techniques soient disponibles dans les extensions standards de **R**, il est souvent préférable
d'avoir recours à deux autres extensions plus complètes, `ade4`{.pkg}
et `FactoMineR`{.pkg}, chacune ayant ses avantages et des possibilités différentes. Voici les fonctions les plus fréquentes :
| Analyse | Variables | Fonction standard | Fonction `ade4`{.pkg} | Fonctions `FactoMineR`{.pkg} |
|:--------|:----------|:-----------------:|:----------------------------------------:|:--------:|
| ACP | plusieurs variables quantitatives | `princomp`{data-pkg="stats"} | `dudi.pca`{data-pkg="ade4"} | `PCA`{data-pkg="FactoMineR"} |
| AFC | deux variables qualitatives | `corresp`{data-pkg="MASS"} | `dudi.coa`{data-pkg="ade4"} | `CA`{data-pkg="FactoMineR"} |
| ACM | plusieurs variables qualitatives | `mca`{data-pkg="MASS"} | `dudi.acm`{data-pkg="ade4"} | `MCA`{data-pkg="FactoMineR"} |
| Analyse mixte | plusieurs variables quantitatives et/ou qualitatives | --- | `dudi.mix`{data-pkg="ade4"} | `FAMD`{data-pkg="FactoMineR"} |
Dans la suite de ce chapitre, nous n'arboderons que l'analyse des correspondances multiples (ACM).
<div class="note">
On trouvera également de nombreux supports de cours en français sur l'analyse factorielle sur le site de
François Gilles Carpentier : <http://geai.univ-brest.fr/~carpenti/>.
</div>
## Principe général
L'analyse des correspondances multiples est une technique descriptive visant à résumer l'information
contenu dans un grand nombre de variables afin de faciliter l'interprétention des corrélations existantes
entre ces différentes variables. On cherche à savoir quelles sont les modalités corrélées entre elles.
L'idée générale est la suivante^[Pour une présentation plus détaillée, voir
<br /><http://www.math.univ-toulouse.fr/~baccini/zpedago/asdm.pdf>.].
L'ensemble des individus peut être représenté dans un espace à plusieurs
dimensions où chaque axe représente les différentes variables utilisées pour décrire chaque individu.
Plus précisément, pour chaque variable qualitative, il y a autant d'axes que de modalités moins un. Ainsi
il faut trois axes pour décrire une variable à quatre modalités. Un tel nuage de points est aussi difficile
à interpréter que de lire directement le fichier de données. On ne voit pas les corrélations qu'il peut y
avoir entre modalités, par exemple qu'aller au cinéma est plus fréquent chez les personnes habitant en
milieu urbain. Afin de mieux représenter ce nuage de points, on va procéder à un changement de systèmes
de coordonnées. Les individus seront dès lors projetés et représentés sur un nouveau système d'axe. Ce
nouveau système d'axes est choisis de telle manière que la majorité des variations soit concentrées sur
les premiers axes. Les deux-trois premiers axes permettront d'expliquer la majorité des différences observées
dans l'échantillon, les autres axes n'apportant qu'une faible part additionnelle d'information. Dès
lors, l'analyse pourra se concentrer sur ses premiers axes qui constitueront un bon résumé des variations
observables dans l'échantillon.
Avant toute ACM, il est indispensable de réaliser une analyse préliminaire de chaque variable, afin
de voir si toutes les classes sont aussi bien représentées ou s'il existe un déséquilibre. L'ACM est sensible
aux effectifs faibles, aussi il est préférable de regrouper les classes peu représentées le cas échéant.
## ACM avec ade4
Si l'extension `ade4`{.pkg} n'est pas présente sur votre PC,
il vous faut l'installer :
```{r, eval=FALSE}
install.packages("ade4", dep = TRUE)
```
Dans tous les cas, il faut penser à la charger en mémoire :
```{r}
library(ade4)
```
Comme précédemment, nous utiliserons le fichier de données `hdv2003` fourni avec l'extension
`questionr`{.pkg}.
```{r}
library(questionr)
data(hdv2003)
d <- hdv2003
```
En premier lieu, comme dans le [chapitre sur la régression logistique](regression-logistique.html),
nous allons créer une variable groupe d'âges et regrouper les modalités de la
variable « niveau d'étude ».
```{r}
d$grpage <- cut(d$age, c(16, 25, 45, 65, 93), right = FALSE, include.lowest = TRUE)
d$etud <- d$nivetud
levels(d$etud) <- c("Primaire", "Primaire", "Primaire", "Secondaire", "Secondaire",
"Technique/Professionnel", "Technique/Professionnel", "Supérieur" )
```
Ensuite, nous allons créer un tableau de données ne contenant que les variables que nous souhaitons
prendre en compte pour notre analyse factorielle.
```{r}
d2 <- d[, c("grpage", "sexe", "etud", "peche.chasse", "cinema", "cuisine", "bricol", "sport", "lecture.bd")]
```
Le calcul de l'ACM se fait tout simplement avec la fonction `dudi.acm`{data-pkg="ade4"}.
```{r, eval=FALSE}
acm <- dudi.acm(d2)
```
Par défaut, la fonction affichera le graphique des <dfn data-index="valeur propre, ACM">valeurs propres</dfn>
de chaque axe (nous y reviendrons) et vous demandera le nombre d'axes que vous souhaitez conserver dans les résultats.
Le plus souvent,
cinq axes seront largement plus que suffisants. Vous pouvez également éviter cette étape en indiquant
directement à `dudi.acm`{data-pkg="ade4"} de vous renvoyer les cinq premiers axes ainsi :
```{r}
acm <- dudi.acm(d2, scannf = FALSE, nf = 5)
```
<div class="note">
Si vous souhaitez explorer visuellement et interacticement les résultats, vous pouvez utiliser l'extension `explor`{.pkg} et sa fonction homonyme `explor`{data-pkg="explor"}.
```{r, eval = FALSE}
explor::explor(acm)
```
</div>
Le graphique des valeurs propres peut être reproduit avec
`screeplot`{data-pkg="ade4" data-rdoc="scatter"} :
<figure>
```{r}
screeplot(acm)
```
<figcaption>Valeurs propres ou inertie de chaque axe avec screeplot()</figcaption>
</figure>
Pour des grahiques reposant sur `ggplot2`{.pkg}, on pourra avoir recours à l'extension `factoextra`{.pkg} qui fournit plusieurs fonctions graphiques dont `fviz_screeplot`{data-pkg="factorextra"}
<figure>
```{r}
library(factoextra)
fviz_screeplot(acm, choice = "eigenvalue")
```
<figcaption>Valeurs propres des axe avec fviz_screeplot()</figcaption>
</figure>
<figure>
```{r}
library(factoextra)
fviz_screeplot(acm)
```
<figcaption>Pourcentage de variance expliquée avec fviz_screeplot()</figcaption>
</figure>
Les mêmes valeurs pour les premiers axes s'obtiennent également avec
`summary`{data-pkg="ade4" data-rdoc="dudi"}. On pourra également avoir recours à la
fonction `inertia.dudi`{data-pkg="ade4"} pour l'ensemble des axes.
```{r}
summary(acm)
inertia.dudi(acm)
```
L'<dfn>inertie</dfn> totale est de 1,451 et l'axe 1 en explique 0,1474 soit 17 %. L'inertie projetée cumulée nous
indique que les deux premiers axes expliquent à eux seuls 29 % des variations observées dans notre
échantillon.
Pour comprendre la signification des différents axes, il importe d'identifier quelles sont les variables/
modalités qui contribuent le plus à chaque axe. Une première représentation graphique est le
<dfn>cercle de corrélation</dfn><dfn data-index="corrélation, cercle"></dfn> des modalités.
Pour cela, on aura recours à `s.corcicle`{data-pkg="ade4"}. On
indiquera d'abord `acm$co` si l'on souhaite représenter les modalités ou `acm$li` si l'on souhaite représenter
les individus. Les deux chiffres suivant indiquent les deux axes que l'on souhaite afficher (dans le cas
présent les deux premiers axes). Enfin, le paramètre `clabel` permet de modifier la taille des étiquettes.
<figure>
```{r}
s.corcircle(acm$co, 1, 2, clabel = 0.7)
```
<figcaption>Cercle de corrélations des modalités sur les deux premiers axes</figcaption>
</figure>
Il est aussi possible d'utiliser `fviz_mca_var`{data-pkg="factoextra"} de `factoextra`{.pkg}. L'option `repel = TRUE` permets d'éviter que les étiquettes ne se superposent.
<figure>
```{r}
fviz_mca_var(acm, repel = TRUE)
```
<figcaption>Représentation des modalités sur les deux premiers axes</figcaption>
</figure>
On pourra avoir également recours à `boxplot`{data-pkg="ade4" data-rdoc="dudi.acm"}
pour visualiser comment se répartissent les modalités
de chaque variable sur un axe donné^[La fonction `score`{data-pkg="ade4" data-rdoc="score.acm"}
constituera également une aide à l'interprétation des axes.].
<figure>
```{r}
boxplot(acm)
```
<figcaption>Répartition des modalités selon le premier axe</figcaption>
</figure>
<figure>
```{r}
boxplot(acm, 2)
```
<figcaption>Répartition des modalités selon le second axe</figcaption>
</figure>
La fonction `fviz_contrib`{data-pkg="factoextra"} de `factoextra`{.pkg} peut être utilisée pour représenter la contribution des différentes variables sur un axe.
<figure>
```{r}
fviz_contrib(acm, choice = "var", axes = 1)
fviz_contrib(acm, choice = "var", axes = 2)
```
<figcaption>Représentation de la contribution des différentes variables</figcaption>
</figure>
Le tableau `acm$cr` contient les rapports de corrélation (variant de 0 à 1) entre les variables
et les axes choisis au départ de l'ACM. Pour représenter graphiquement ces rapports, utiliser la
fonction `barplot`{data-pkg="graphics"} ainsi :
`barplot(acm$cr[,num],names.arg=row.names( acm$cr),las=2)` où `num` est le numéro de l'axe à représenter.
Pour l'interprétation des axes, se concentrer sur les variables les plus
structurantes, c'est-à-dire dont le rapport de corrélation est le plus proche de 1.
<figure>
```{r}
par(mfrow = c(2, 2))
for (i in 1:4) barplot(acm$cr[, i], names.arg = row.names(acm$cr), las = 2, main = paste("Axe", i))
par(mfrow = c(1, 1))
```
<figcaption>Rapports de corrélation des variables sur les 4 premiers axes</figcaption>
</figure>
<div class="note">
Le paramètre `mfrow` de la fonction `par`{data-pkg="graphics"} permet d'indiquer à **R**
que l'on souhaite afficher plusieurs graphiques sur une seule et même fenêtre, plus précisément
que l'on souhaite diviser la fenêtre en deux lignes et deux colonnes.
Dans l'exemple précédent, après avoir produit notre graphique, nous avons réinitilisé cette valeur
à `c(1, 1)` (un seul graphique par fenêtre) pour ne pas affecter les prochains graphiques que nous
allons produire.
</div>
Pour représenter, les modalités dans le <dfn>plan factoriel</dfn><dfn data-index="factoriel, plan"></dfn>,
on utilisera la fonction `s.label`{data-pkg="ade4"}. Par défaut, les deux premiers axes sont représentés.
<figure>
```{r}
s.label(acm$co, clabel = 0.7)
```
<figcaption>Répartition des modalités selon les deux premiers axes</figcaption>
</figure>
Il est bien sur possible de préciser les axes à représenter. L'argument `boxes` permet
quant à lui d'indiquer si l'on souhaite tracer une boîte pour chaque modalité.
<figure>
```{r}
s.label(acm$co, 3, 4, clabel = 0.7, boxes = FALSE)
```
<figcaption>Répartition des modalités selon les axes 3 et 4</figcaption>
</figure>
Bien entendu, on peut également représenter les individus. En indiquant `clabel=0`
(une taille nulle pour les étiquettes), `s.label`{data-pkg="ade4"} remplace chaque observation
par un symbole qui peut être spécifié avec `pch`.
<figure>
```{r}
s.label(acm$li, clabel = 0, pch = 17)
```
<figcaption>Répartition des individus selon les deux premiers axes</figcaption>
</figure>
<div class="note">
L'agument `pch` permet de spécifier le symbole à utiliser.
Il peut prendre soit un nombre entier compris entre 0 et 25, soit un charactère textuel.
```{r, echo=FALSE}
source("data/pchShow.R")
pchShow(
c("*","+","a","x"), main = "Différentes valeurs possibles pour l'argument pch",
symbolsize = 2.5, linewidth = 2, fillcolor = "palegreen3", symbolcolor = "palevioletred3"
)
```
</div>
Il est également possible d'avoir recours à `fviz_mca_ind`{data-pkg="factoextra"} de `factoextra`{.pkg}. `geom = "point"` permets de de ne réprésenter que les points sans leur étiquette. `alpha.ind = .25` permets d'appliquer une transparance.
<figure>
```{r}
fviz_mca_ind(acm, geom = "point", alpha.ind = .25)
```
<figcaption>Répartition des individus selon les deux premiers axes avec fviz_mca_ind()</figcaption>
</figure>
<div class="note">
Lorsque l'on réalise une ACM, il n'est pas rare que plusieurs observations soient identiques, c'est-à-dire
correspondent à la même combinaison de modalités. Dès lors, ces observations seront projetées sur le
même point dans le plan factoriel. Une représentation classique des observations avec
`s.label`{data-pkg="ade4"} ne permettra pas de rendre compte les effectifs de chaque point.
Le package `JLutils`{.pkg}, disponible seulement sur
**[GitHub](https://github.com/larmarange/JLutils)**, propose une fonction `s.freq`{data-pkg="JLutils"}
représentant chaque point par un carré proportionnel au nombre d'individus.
Pour installer `JLutils`{.pkg}, on aura recours au package
`devtools`{.pkg} et à sa fonction `install_github`{data-pkg="devtools"} :
```{r, eval=FALSE}
library(devtools)
install_github("larmarange/JLutils")
```
La fonction `s.freq`{data-pkg="JLutils"} s'emploie de manière similaire aux autres fonctions
graphiques de `ade4`{.pkg}. Le paramètre `csize` permet d'ajuster
la taille des carrés.
```{r}
library(JLutils)
s.freq(acm$li)
```
L'interprétation est tout autre, non ?
</div>
<div class="note">
Gaston Sanchez propose un graphique amélioré des modalités dans le plan factoriel, avec notamment de coubes de densité, à cette adresse :
<http://rpubs.com/gaston/MCA>.
</div>
La fonction `s.value`{data-pkg="ade4"} permet notamment de représenter un troisième axe factoriel.
Dans l'exemple ci-après, nous projettons les individus selon les deux premiers axes factoriels.
La taille et la couleur des carrés dépendent pour leur part de la coordonnée des individus sur le
troisième axe factoriel. Le paramètre `csi` permet d'ajuster la taille des carrés.
<figure>
```{r}
s.value(acm$li, acm$li[, 3], 1, 2, csi = 0.5)
```
<figcaption>Répartition des individus selon les trois premiers axes</figcaption>
</figure>
`s.arrow`{data-pkg="ade4"} permet de représenter les vecteurs variables ou les vecteurs individus
sous la forme d'une flèche allant de l'origine du plan factoriel aux coordonnées des variables/individus :
<figure>
```{r}
s.arrow(acm$co, clabel = 0.7)
```
<figcaption>Vecteurs des modalités selon les deux premiers axes</figcaption>
</figure>
`s.hist`{data-pkg="ade4"} permet de représenter des individus (ou des modalités) sur le plan
factoriel et d'afficher leur distribution sur chaque axe :
<figure>
```{r, results='hide'}
s.hist(acm$li, clabel = 0, pch = 15)
```
<figcaption>Distribution des individus dans le plan factoriel</figcaption>
</figure>
`s.class`{data-pkg="ade4"} et `s.chull`{data-pkg="ade4"} permettent de représenter
les différentes observations classées en plusieurs catégories.
Cela permet notamment de projeter certaines variables.
`s.class`{data-pkg="ade4"} représente les observations par des points, lie chaque
observation au barycentre de la modalité à laquelle elle appartient et dessine une
ellipse représentant la forme générale du nuage de points :
<figure>
```{r}
library(RColorBrewer)
s.class(acm$li, d2$sexe, col = brewer.pal(4, "Set1"))
```
<figcaption>Individus dans le plan factoriel selon le sexe (s.class)</figcaption>
</figure>
`s.chull`{data-pkg="ade4"} représente les barycentres de chaque catégorie et dessine
des lignes de niveaux représentant la distribution des individus de cette catégorie.
Les individus ne sont pas directement représentés :
<figure>
```{r}
s.chull(acm$li, d2$sexe, col = brewer.pal(4, "Set1"))
```
<figcaption>Individus dans le plan factoriel selon le sexe (s.chull)</figcaption>
</figure>
<div class="note">
Il est préférable de fournir une liste de couleurs (via le paramètre `col`) pour rendre le graphique plus
lisible. Si vous avez installé l'extension `RColorBrewer`{.pkg}, vous pouvez
utiliser les différentes palettes de couleurs proposées.
Pour afficher les palettes disponibles, utilisez
`display.brewer.all`{data-pkg="RColorBrewer" data-rdoc="RColorsBrewer"}.
```{r, fig.height=8, fig.wid2h=8}
library(RColorBrewer)
display.brewer.all(8)
```
Pour obtenir une <dfn>palette de couleurs</dfn><dfn data-index="couleur, palette"></dfn>, utilisez la fonction
`brewer.pal`{data-pkg="RColorBrewer" data-rdoc="RColorsBrewer"} avec les arguments
`n` (nombre de couleurs demandées) et `pal`(nom de la palette de couleurs désirée).
Pour plus d'informations sur les palettes de couleurs de **R**, voir le [chapitre dédié](couleurs.html).
</div>
Il est aussi possible de passer à `fviz_mca_ind`{data-pkg="factoextra"} une variable de regroupement via le paramètre `habillage`.
<figure>
```{r}
fviz_mca_ind(acm, geom = "point", alpha.ind = .25, habillage = d2$sexe, addEllipses = TRUE)
```
<figcaption>Individus dans le plan factoriel selon le sexe (fviz_mca_ind)</figcaption>
</figure>
La variable catégorielle transmise à `s.class`{data-pkg="ade4"} ou `s.chull`{data-pkg="ade4"}
n'est pas obligatoirement une des variables retenues pour l'ACM.
Il est tout à fait possible d'utiliser une autre variable. Par exemple :
<figure>
```{r}
s.class(acm$li, d$trav.imp, col = brewer.pal(4, "Set1"))
```
<figcaption>Individus dans le plan factoriel selon l'importance donnée au travail</figcaption>
</figure>
Les fonctions `scatter`{data-pkg="ade4"} et
`biplot`{data-pkg="ade4" data-rdoc="scatter"} sont équivalentes :
elles appliquent `s.class`{data-pkg="ade4"} à chaque variable utilisée pour l'ACM.
<figure>
```{r}
scatter(acm, col = brewer.pal(4, "Set1"))
```
<figcaption>La fonction scatter appliquée au résultat d'une ACM</figcaption>
</figure>
## ACM avec FactoMineR{#factominer}
Comme avec `ade4`{.pkg}, il est nécessaire de préparer les données au préalable
(voir section précédente).
L'ACM se calcule avec la fonction `MCA`{data-pkg="FactoMineR"}, l'argument `ncp` permettant de choisir
le nombre d'axes à retenir :
```{r, warning=FALSE, message=FALSE}
library(FactoMineR)
```
```{r}
acm2 <- MCA(d2, ncp = 5, graph = FALSE)
acm2
acm2$eig
sum(acm2$eig[, 1])
```
En premier lieu, il apparait que l'inertie totale obtenue avec `MCA`{data-pkg="FactoMineR"} est
différente de celle observée avec `dudi.acm`{data-pkg="ade4"}. Cela est dû à un traitement différents
des <dfn data-index="valeur manquante">valeurs manquantes</dfn><dfn data-index="manquante, valeur"></dfn>.
Alors que `dudi.acm`{data-pkg="ade4"} exclu les
valeurs manquantes, `MCA`{data-pkg="FactoMineR"} les considèrent, par défaut, comme une modalité
additionnelle. Pour calculer l'ACM uniquement sur les individus n'ayant pas de valeur manquante, on aura recours à `complete.cases`{data-pkg="stats"} :
```{r}
acm2 <- MCA(d2[complete.cases(d2), ], ncp = 5, graph = FALSE)
acm2$eig
sum(acm2$eig[, 1])
```
Les possibilités graphiques de `FactoMineR`{.pkg} sont différentes de celles de
`ade4`{.pkg}. Un recours à la fonction
`plot`{data-pkg="FactoMineR" data-rdoc="plot.MCA"} affichera par défaut les individus,
les modalités et les variables. La commande `?plot.MCA` permet d'accéder au fichier d'aide de cette fonction
(i.e. de la méthode générique `plot` appliquée aux objets de type `MCA`) et de voir toutes
les options graphiques. L'argument `choix` permet de spécifier ce que l'on souhaite afficher (« ind »
pour les individus et les catégories, « var » pour les variables). L'argument `invisible` quant à lui permet
de spécifier ce que l'on souhaite masquer. Les axes à afficher se précisent avec `axes`. Voir les exemples
ci-dessous.
<figure>
```{r}
plot(acm2)
```
<figcaption>Plan factoriel (deux premiers axes)</figcaption>
</figure>
<figure>
```{r}
plot(acm2, axes = c(3, 4))
```
<figcaption>Plan factoriel (axes 3 et 4)</figcaption>
</figure>
<figure>
```{r}
plot(acm2, choix = "ind")
```
<figcaption>Plan factoriel (seulement les individus et les catégories)</figcaption>
</figure>
<figure>
```{r}
plot(acm2, choix = "ind", invisible = "ind")
```
<figcaption>Plan factoriel (seulement les catégories)</figcaption>
</figure>
<figure>
```{r}
plot(acm2, choix = "var")
```
<figcaption>Plan factoriel (seulement les variables)</figcaption>
</figure>
La fonction `plotellipses`{data-pkg="FactoMineR"} trace des ellipses de confiance atour des
modalités de variables qualitatives. L'objectif est de voir si les modalités d'une variable
qualitative sont significativement différentes les unes des autres.
Par défaut (`means=TRUE`), les ellipses de confiance sont calculées pour les coordonnées moyennes
de chaque catégorie.
<figure>
```{r}
plotellipses(acm2)
```
<figcaption>Ellipses de confiance (means=TRUE) dans le plan factoriel</figcaption>
</figure>
L'option `means=FALSE` calculera les ellipses de confiance
pour l'ensemble des coordonnées des observations relevant de chaque catégorie.
<figure>
```{r}
plotellipses(acm2, means = FALSE)
```
<figcaption>Ellipses de confiance (means=FALSE) dans le plan factoriel</figcaption>
</figure>
La fonction `dimdesc`{data-pkg="FactoMineR"} aide à décrire et interpréter les dimensions de l'ACM.
Cette fonction est très utile quand le nombre de variables est élevé.
Elle permet de voir à quelles variables les axes sont le plus
liés : quelles variables et quelles modalités décrivent le mieux chaque axe ?
> Pour les variables qualitatives, un modèle d'analyse de variance à un facteur est réalisé pour chaque
> dimension ; les variables à expliquer sont les coordonnées des individus et la variable explicative est une
> des variables qualitatives. Un test F permet de voir si la variable a un effet significatif sur la dimension
> et des tests T sont réalisés modalité par modalité (avec le contraste somme des alpha_i=0). Cela montre
> si les coordonnées des individus de la sous-population définie par une modalité sont significativement
> différentes de celles de l'ensemble de la population (*i.e.* différentes de 0). Les variables et modalités sont
> triées par probabilité critique et seules celles qui sont significatives sont gardées dans le résultat.
>
> <footer>Source : <http://factominer.free.fr/factosbest/description-des-dimensions.html></footer>
```{r, eval=FALSE}
dd <- dimdesc(acm2, axes = 1:2)
dd$`Dim 1`
```
## Extensions complémentaires
### factoextra
L'extension `factoextra`{.pkg} fournit des fonctions graphiques `ggplot2`{.pkg} pour visualiser les résultats d'une analyse factorielle, réalisée avec `ade4`{.pkg} ou `FactoMineR`{.pkg}.
Plus d'informations sur <https://rpkgs.datanovia.com/factoextra/>.
### explor
L'extension `explor`{.pkg} fournit une interface graphique pour explorer les résultats d'une analyse factorielle, réalisée avec `ade4`{.pkg} ou `FactoMineR`{.pkg}.
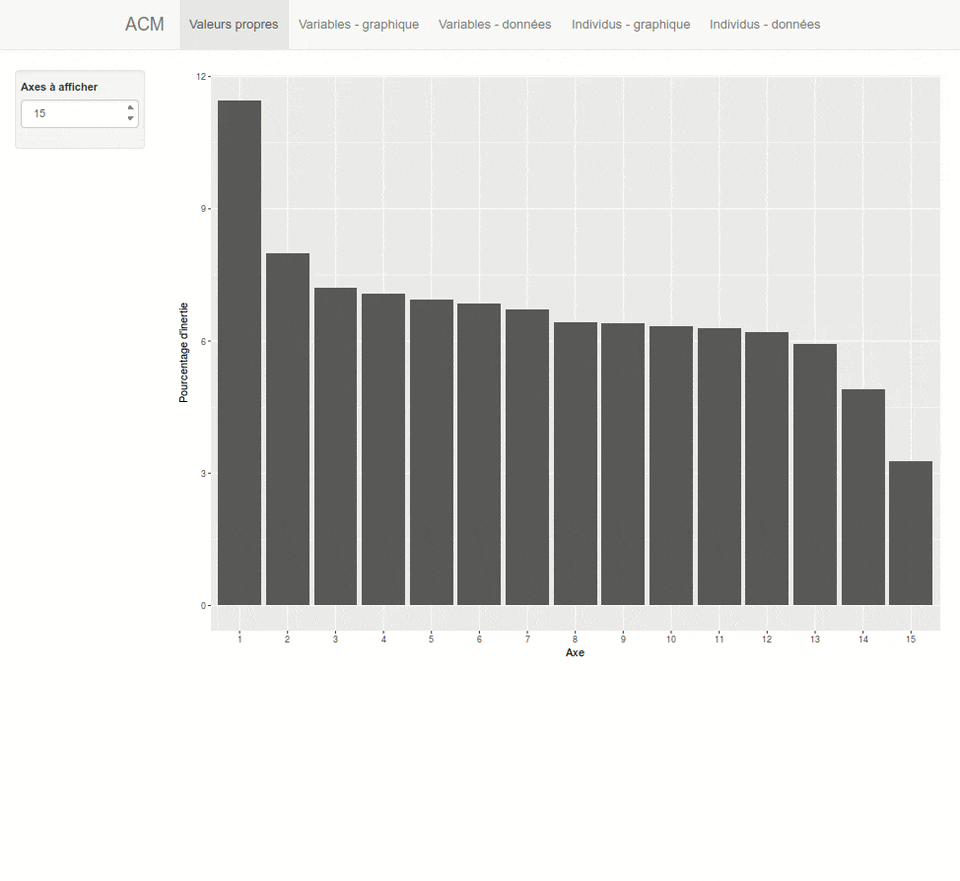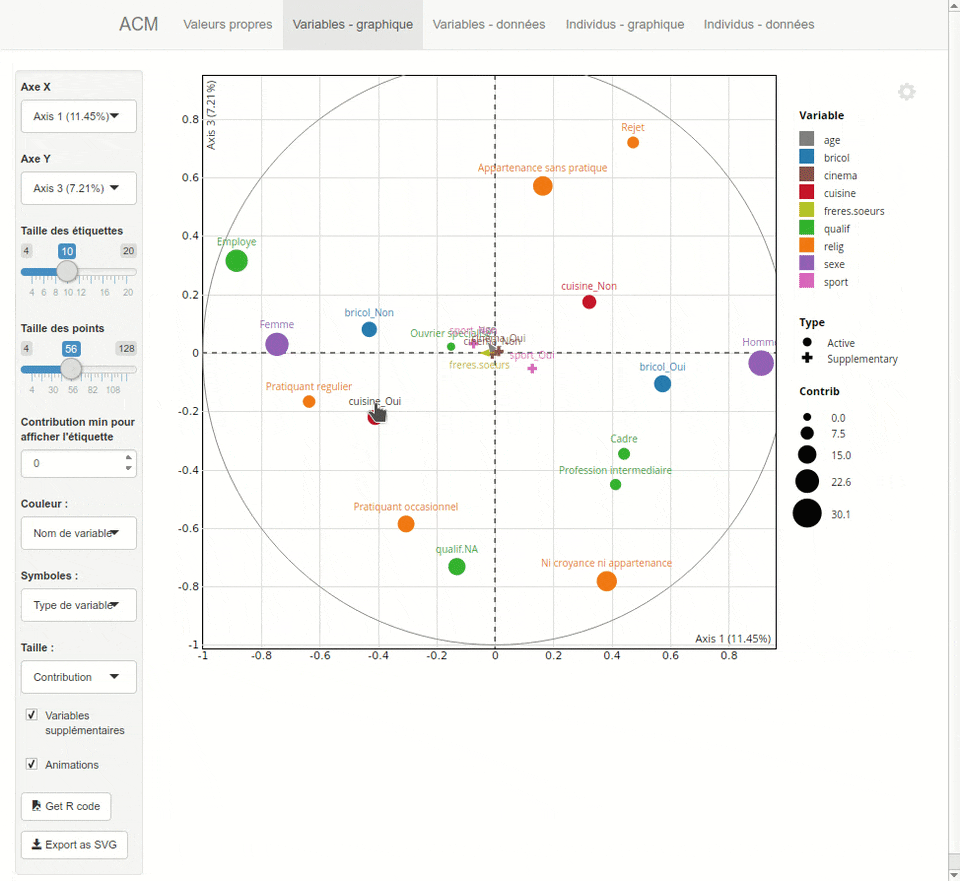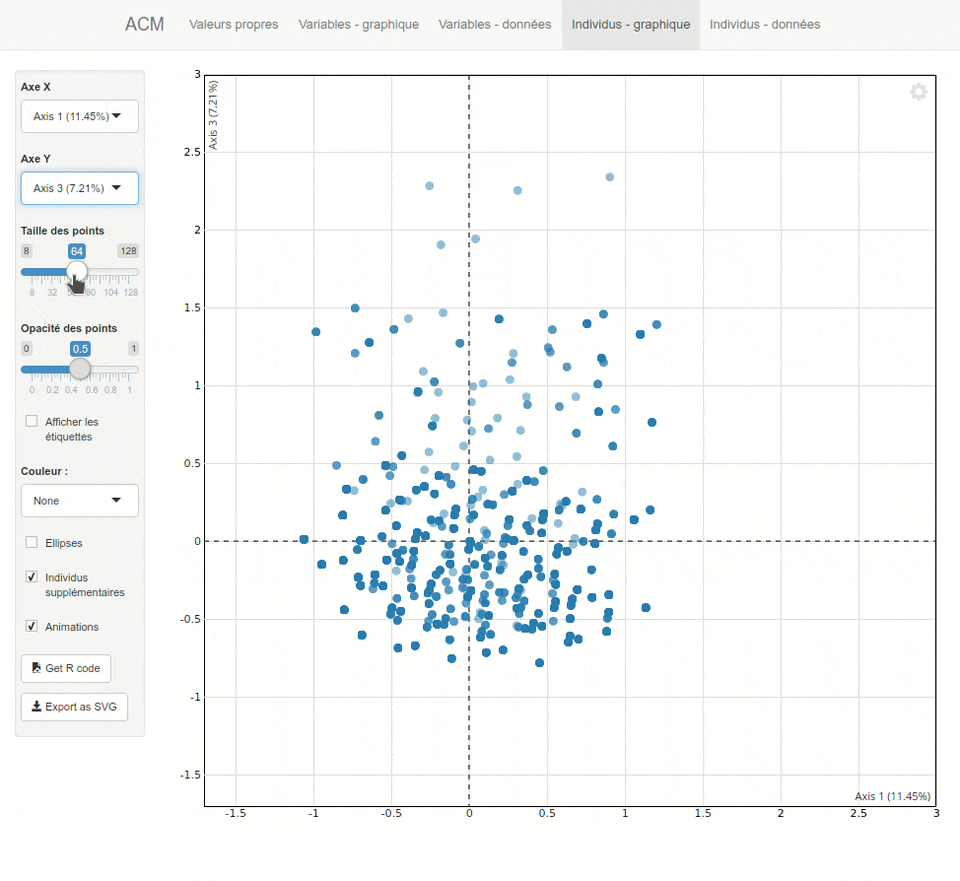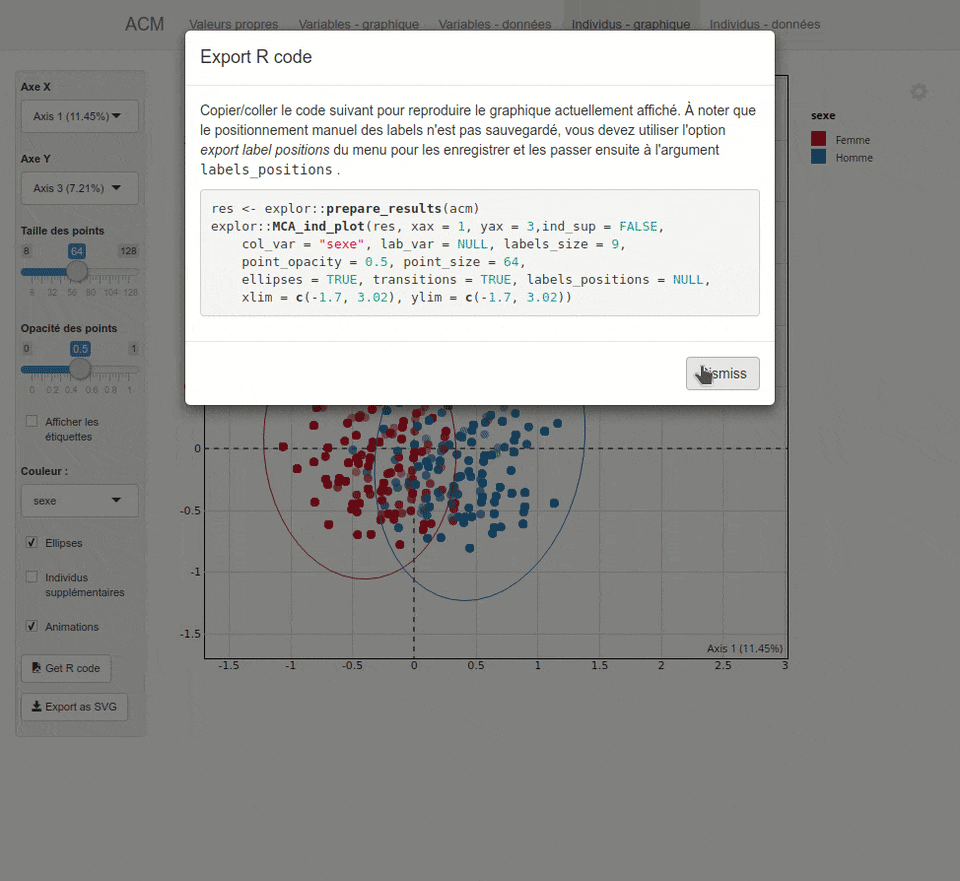
Plus d'informations sur <https://github.com/juba/explor/>.
### GDAtools
L'extension `GDAtools`{.pkg} développé par Nicolas Robette propose plusieurs outils pour l'interprétation et la visualisation des analyses factorielles ainsi que différentes variables d'ACM, pour la prise en compte par exemple des valeurs manquantes.
On pourra se référer au tutoriel dédié disponible en français sur <https://nicolas-robette.github.io/GDAtools/articles/french/Tutoriel_AGD.html>.
### Factoshiny
L'extension `Factoshiny`{.pkg} permet d'améliorer facilement et de façon interactive les graphiques produits par `FactoMineR`{.pkg} pour les rendre beaucoup plus lisibles.
Plus d'informations sur <http://factominer.free.fr/graphs/factoshiny-fr.html>.
### FactoInvestigate
L'extension `FactoInvestigate`{.pkg} décrit et interprète automatiquement les résultats de votre analyse factorielle (ACP, AFC ou ACM) en choisissant les graphes les plus appropriés pour un rapport.
Vous avez juste à faire l'analyse comme habituellement avec `FactoMineR`{.pkg} ou `Factoshiny`{.pkg}, et ensuite utiliser `FactoInvestigate`{.pkg} pour obtenir un rapport automatisé.
Plus d'informations sur <http://factominer.free.fr/reporting/index_fr.html>.
## Voir aussi
Un tutoriel détaillé en français, <q>Visualiser une analyse géométrique des données avec ggplot2 (R/RStudio)</q>, est disponible sur le blog Quanti : <https://quanti.hypotheses.org/1871>.