Finite Difference Pricing: A C++ application of the Crank Nicolson scheme for pricing dividend paying American Options by means of the Green Function
This repository implements a practical application of the Crank Nicolson scheme for pricing American Options by means of the Green Function.
Whilst binomial and trinomial lattices are very popular in the stock option pricing framework, I believe that a Finite Difference setup has greater flexibility in terms of model choice (e.g. Black-Scholes), without giving up too much throughput.
I worked on the numerical solution of the Kolmogorov equation using the Method of Line (MoL), where the space discretization follows the central point scheme for second and first order derivatives. As per the time solver, I decided to implement the 3 easiest method I could think of: Explicit and Implicit Euler, and the Crank Nicolson scheme. If one wants to implement a more accurate method such as one in the Runge Kutta family, the method CEvolutionOperator<>::Apply(...) can be amended accordingly.
I implemented this having in mind a single-threaded framework, meaning that a thread is responsible to price an option without spawning other threads. That is why I decided not to use any 3rd party library for Linear Algebra, and I decided to implement some few methods (namely the dot product and the Thomas Algorithm for solving a tridiagonal system) myself. Nevertheless, using some compiler options (Graphite, Polly, or the Intel built-in parallelization) it is possible to obtain an auto-parallelized version of the code.
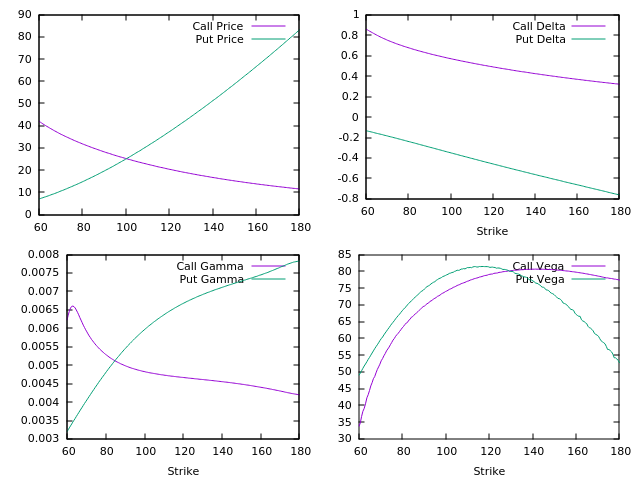
As regards the functionality, this library prices European or American option with cash dividends. The payoff smoothing and the acceleration techniques are well-known for the Binomial Tree, and I decided to make use of them. The space grid choice can be either linear, logarithmic or concentraded towards a reference value (with that being either the spot or the strike), following Tavella-Randall paper. The time grid is instead a linear space, where it is refined whenever a dividend is encountered. I made use of Adjoint Differentiation for calculating Vega and Rho without re-calculating the evolution operators. As a plotting tool, I decided to use GNU plot.
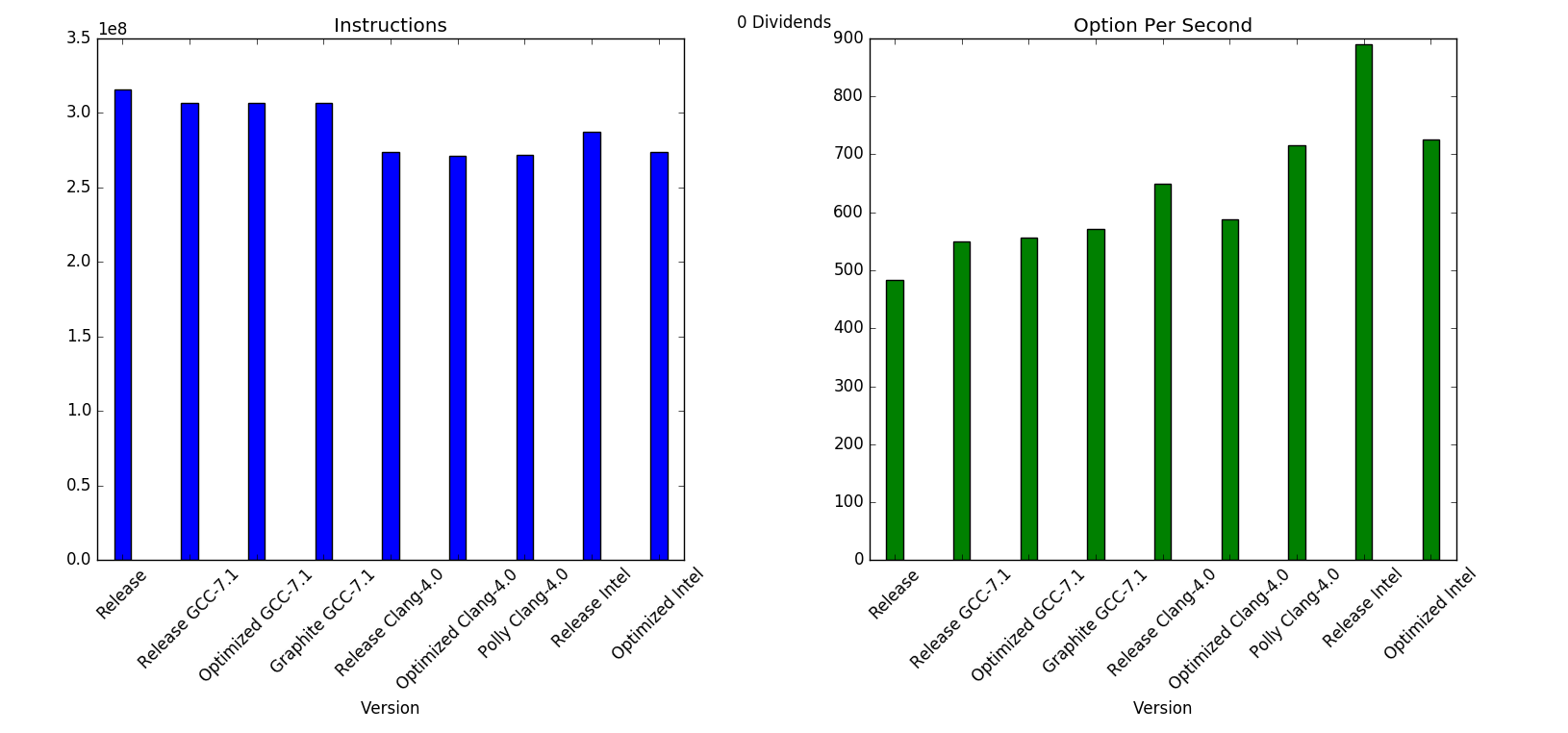
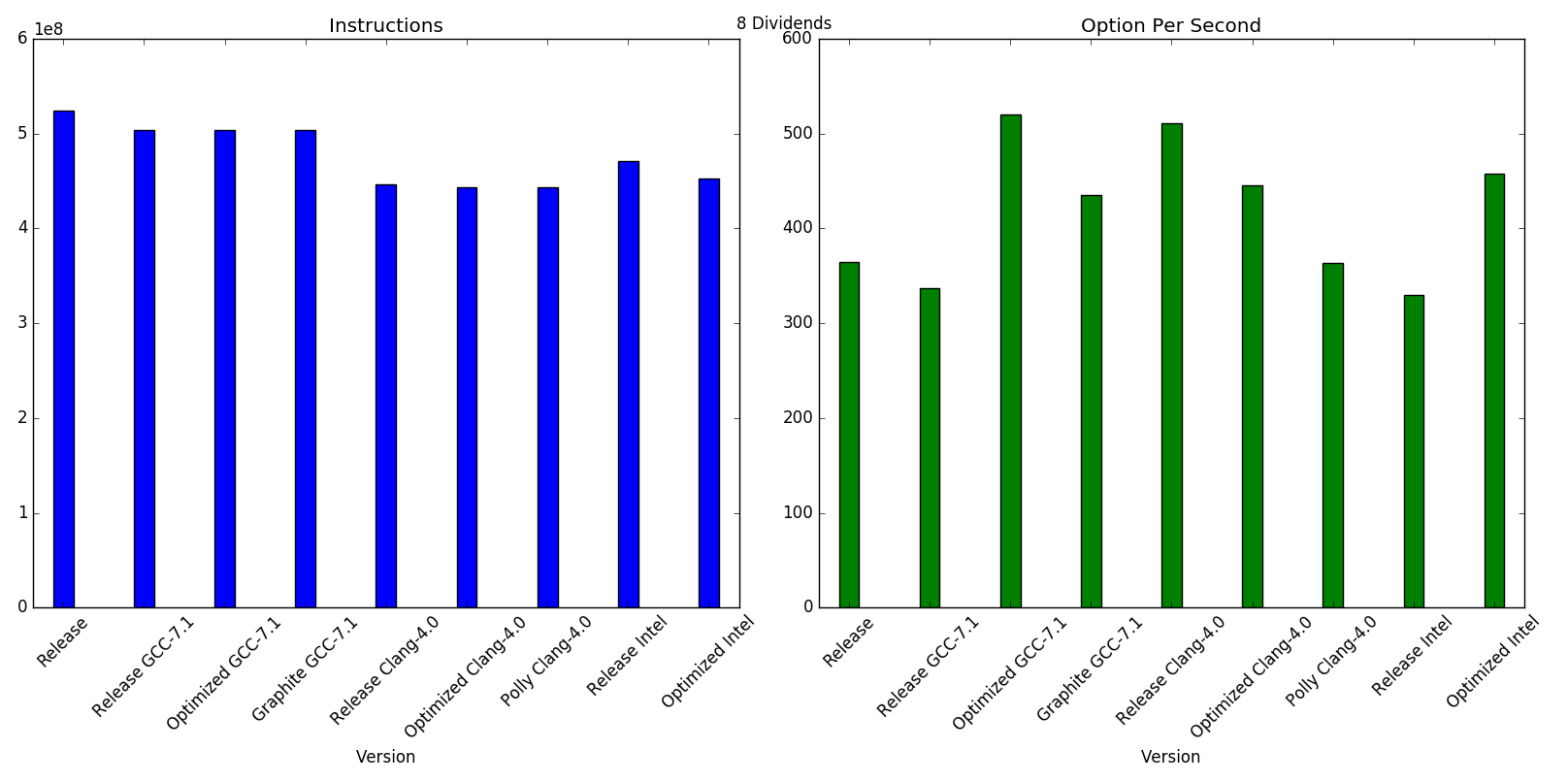
As regards the performance, I haven't spent time into optimizing the code, this is pretty much the first iteration. I included some Callgrind output to spot the hottest functions, but intuitevely most of the time is spent in inverting tridiagonal matrices. Just for fun I've tried different compilers with different settings, and I've also run some performance testing in my laptop.
For further analysis, I've written a Python script that compiles and run callgrind on each configuration and gathers the results.
I've implemented this project using Eclipse IDE for generating Makefiles. So each configuration has got a separate folder with its own Makefile. I have tried the following configurations:
- GCC (the default one in my laptop was 5.1.0)
- GCC 7.1.0
- Clang 4.0
- ICC 17.0
The Release mode is just a plain -O3. The Optimized mode was just my attempt of finding the most effective set of optimization flag to pass onto each compiler. I dind't spend too much time on it, so it might be as well possible that the flags that I am using are not optimal; it was nevertheless interesting to see the effect of each individual flag (if any) on the final results. The sets of flags that I've used are:
- GCC-7.1.0: O3 -march=native
- Clang 4.0: O3 -ffast-math -march=native
- Graphite (with Link Time Optimization): -O3 -march=native -flto=8 -floop-interchange -ftree-loop-distribution -floop-strip-mine -floop-block -ftree-vectorize
- Polly: O3 -ffast-math -march=native -mllvm -polly -mllvm -polly-vectorizer=stripmine
- ICC: O3 -no-prec-div -no-prec-sqrt -ansi-alias -xHost -ipo -fp-model fast=2 -fimf-precision=low -vec-threshold=80 -qopt-report3 -fno-alias
It is worth saying that the options that modify FP accuracy (e.g. fast math) didn't break any test, so I decided to try them on. Again, no conclusion can be said based on these experiment, but it was fun to try. The set of default flags that I've used are:
- pedantic -pedantic-errors -Wall -Wextra -Werror for catching every possible warning
- -pipe for trying to make compilation a tiny bit faster
- -fstrict-aliasing as I do not generally alias memory locations
- -fPIC