-
Notifications
You must be signed in to change notification settings - Fork 239
Presentation denotational payment



⚠ This file is automatically generated from this org file using this script.
The exported presentation can be accessed via this githack link.
REVISIONS:
| Date | Notes |
| 2022-07-13 | First quick draft for guardtime visit |
| 2022-07-29 | Re-drated for the lambda days 2022 |
- A new payment paradigm:
- where money can be instantly or continuously moved from 1-to-1 or 1-to-N en-mass.
- How a Haskell toy model/reference implementation/specification for it is written:
- Haskell - A pure, strongly-typed, syntactically terse language best suited for domain modeling.
- “A domain model is a conceptual model of the domain that incorporates both behavior and data.”
- Also similar to what Conal Elliot advocated for: a denotational design of software.
- A teaser of new perspectives on money,
- Let’s search for some categories related to money.
- Real time finance, a new area for innovations.
Bob requests to send €42 to Alice now.
Bob requests to send a constant flow of money at €420 per 30 day to Alice now.
Microsoft requests to send $0.42 per share to all its share holders on the next ex-dividend date.
Elon Musk requests to send a constant flow of money at €4.2B per 360 days to all its share holders with individual flow rates proportional to their number of share units, from 20st April.
- Financial Market Utilities (FMUs): SEPA, TARGET2, Fedwire, CHIPS, SWIFT, etc. [fn:fmus]
- Public Blockchains and their token standards: Bitcoin, Ethereum, Ethereum ERC-20 tokens, etc.
| FMUs | Public blockchain | |
|---|---|---|
| Instant | Yes, fast within the system, poor interoperability | Yes, with scalability issue |
| Streaming | Micro transactions | Micro transactions, but can be costly on some system |
| en mass | NOPE | Some system may have ad-hoc implementations. |
-
FORMAL SPECIFICATION
- A foundation designed using denotational semantics approach. (Conal Elliott/Lambda Jam 2015)
- Built with compositionality in mind. (Simon Peyton Jones/Microsoft research, “Composing contracts”)
-
EFFICIENT
- A system that interprets the DSL and performs the operations with as little as possible information waste.
- Use micro payments to simulate flow of money? NOPE
- Send dividens payment one by one to all share holders? NOPE
- They are all too noisy.
- A system that interprets the DSL and performs the operations with as little as possible information waste.
- Design an denotational semantics for new payment requests.
- An expressive and composable DSL for the semantics.
- A new payment rail that natively interprets and execute the DSL.

How money is represented in the system?

class (Integral v, Default v) => Value v- But there are no further “types” of value.
- Let us call these values unaccounted for.
- We give value a tag, so that it can be accounted for by sub systems.
- We will see what are sub systems later…
-- | Typed value is an otherwise unaccounted value ~v~ with an associated ~vtag~.
class ( TypedValueTag vtag
, Value v
) => TypedValue tv vtag v | tv -> v, tv -> vtag where
untypeValue :: tv -> v
default untypeValue :: Coercible tv v => tv -> v
untypeValue = coerce
-- | Tag for typed value type class using ~Typeable~ runtime information.
class Typeable vtag => TypedValueTag vtag where
tappedValueTag :: Proxy vtag -> String- There are two sub classes of typed values:
- Untapped typed value doesn’t have a designated sub system. Hence any sub system can add or remove amount of this type.
- Any tapped typed value on the other hand is designed to a specific sub system. Hence only that sub system can add or remove amount of this type.
- An example is that, in your personal account, untapped typed value is what you can still use, while tapped typed value is what is reserved by the bank for a future transaction.
-- | Untapped value type. It can be freely accessed by any sub systems. newtype UntappedValue v = UntappedValue instance Value v => TypedValue (UntappedValue v) UntappedValueTag v -- | Tapped value tag. It must only be accessed by its designated sub system. class TypedValueTag tvtag => TappedValueTag tvtag instance (Value v, TypedValueTag vtag) => TypedValue (TappedValue vtag v) vtag v
- Let’s call a functorful of these typed value
RealTimeBalance. - Or simply view it is a list of typed values
[untapped value, tapped value 1, tapped value 2, ...].
class ( Value v
, Foldable rtbF
, Monoid (rtbF v)
) => RealTimeBalance rtbF v | v -> rtbF where
-- | Convert a single monetary value to a RTB value.
valueToRTB :: v -> rtbF v
-- | Net monetary value of a RTB value.
netValueOfRTB :: rtbF v -> v
netValueOfRTB = foldr (+) def
-- | Convert typed values to a RTB value.
typedValuesToRTB :: UntappedValue v -> [AnyTappedValue v] -> rtbF v
-- | Get typed values from a RTB value.
typedValuesFromRTB :: rtbF v -> (UntappedValue v, [AnyTappedValue v])-- monoid laws
monoid_right_identity x = (x <> mempty) `sameAs` x
monoid_left_identity x = (mempty <> x) `sameAs` x
monoid_associativity a b c = ((a <> b) <> c) `sameAs` (a <> (b <> c))
-- in addition to monoid laws, it also has some other nice properties:
monoid_mappend_commutativity a b =
(a <> b) `sameAs` (b <> a)
rtb_identity_from_and_to_typed_values x = -- type of x is a RealTimeBalance
(uncurry typedValuesToRTB . typedValuesFromRTB) x `sameAs` x
rtb_conservation_of_net_value x = -- type of x is a Value
(netValueOfRTB . valueToRTB) x == x- U is the set of monetary units.
- ν : U → N is the value function.
- β : U → B is the bearer function.
- Monetary unit examples: coins, bank notes, bank account, crypto wallet, etc.

Cit. buldas2021unifying - A Unifying Theory of Electronic Money and Payment Systems
- ν needs an additional input ctx, known as the context.
- ctx should be some value that’s “shared” globally in nature.
- For example, it could be timestamp.
- Further more, ν returns a RTB instead of the unaccounted value type.


How money should be moved in the system?

- Let us define another concept “agreement”, to represent on-going relationships between monetary units.
- It has two parts:
- Agreement Monetary Unit Data.
- Agreement Operation.
- It provides part of the real time balance for the monetary unit.
class ( SuperfluidTypes sft
, Monoid amud -- !! A MONOID, so that system may scale
) => AgreementMonetaryUnitData amud sft | amud -> sft where
-- | π function -
-- balance provided (hear: π) by the agreement monetary unit data.
balanceProvidedByAgreement
:: amud -- amud
-> SFT_TS sft -- t !! THIS IS WHAT MAKES THINGS REAL TIME
-> SFT_RTB sft -- rtb
-- | Calculate the real time balance of an monetary unit at a given time.
balanceOfAt :: (SuperfluidTypes sft, MonetaryUnit mu sft)
=> mu -> SFT_TS sft -> SFT_RTB sft
balanceOfAt mu t = foldr -- !! THIS IS THE: ν(u, t)
-- !! providedBalanceByAnyAgreement is the balanceProvidedByAgreement for the existential type
-- returned from agreementsOf.
((<>) . (flip (providedBalanceByAnyAgreement mu) t))
mempty
(agreementsOf mu)- They are the little engines that make values move.
class ( SuperfluidTypes sft
, AgreementMonetaryUnitData (AgreementMonetaryUnitDataInOperation ao) sft
) => AgreementOperation ao sft | ao -> sft where
-- ... for brevity, removed some type definitions here...
-- | ω function - apply agreement operation ~ao~ (hear: ω) onto the agreement
-- operation data ~aod~ to get a tuple of:
--
-- 1. An updated ~aod'~.
-- 2. A functorful delta of agreement monetary unit data ~aorΔ~, which then
-- can be monoid-appended to existing ~amud~. This is what can make an
-- agreement scalable.
applyAgreementOperation
:: amud ~ (AgreementMonetaryUnitDataInOperation ao)
=> ao -- ao
-> AgreementOperationData ao -- aod
-> SFT_TS sft -- t
-> ( AgreementOperationData ao
, AgreementOperationResultF ao amud) -- (aod', aorΔ)
Semantic: Party A sends an X amount of money instantly to party B.
- Built from lenses.
- TLDR: Lens’ is a data structure of a pair of getter and setter.
class (Default amuLs, SuperfluidTypes sft)
=> MonetaryUnitLenses amuLs sft | amuLs -> sft where
untappedValue :: Lens' amuLs (UntappedValue (SFT_MVAL sft))newtype Operation sft = Transfer (SFT_MVAL sft)
instance SuperfluidTypes sft => AgreementOperation (Operation sft) sft where
data AgreementOperationResultF (Operation sft) elem = OperationPartiesF
{ transferFrom :: elem
, transferTo :: elem
} deriving stock (Functor, Foldable, Traversable)
applyAgreementOperation (Transfer amount) acd _ = let
acd' = acd
aorΔ = fmap ITMUD.MkMonetaryUnitData (OperationPartiesF
(def & set ITMUD.untappedValue (coerce (- amount)))
(def & set ITMUD.untappedValue (coerce amount)))
in (acd', aorΔ)- monoid
instance MonetaryUnitLenses amuLs sft
=> Semigroup (MonetaryUnitData amuLs sft) where
(<>) (MkMonetaryUnitData a) (MkMonetaryUnitData b) =
let c = a & over untappedValue (+ b^.untappedValue)
in MkMonetaryUnitData c
instance MonetaryUnitLenses amuLs sft
=> Monoid (MonetaryUnitData amuLs sft) where
mempty = MkMonetaryUnitData def- π function
instance MonetaryUnitLenses amuLs sft
=> AgreementMonetaryUnitData (MonetaryUnitData amuLs sft) sft where
balanceProvidedByAgreement (MkMonetaryUnitData a) _ =
typedValuesToRTB (a^.untappedValue) []-
SF.transferuses theITA.Operationdefined above, this is how its semantic looks like:
runToken token $ SF.transfer (ITA.OperationPartiesF bob alice) (USD 42)Well, we just redefined 1to1 instant payment using this new semantic… big deal, what’s next?
Semantic: Party A sends a flow of money at a constant rate X to party B.
- How can it work in a nut shell?
- A and B shares the same context “time”, when time advances A & B’s balances move at the same rate but opposite direction for both of them, for one single CFA agreement.
- Any party can have as many such CFA agreements on going as needed, its all in one single value: net flow rate for the party. Thanks to the monoid structure, it is very scalable.
class (Default amuLs, SuperfluidTypes sft)
=> MonetaryUnitLenses amuLs sft | amuLs -> sft where
settledAt :: Lens' amuLs (SFT_TS sft)
settledUntappedValue :: Lens' amuLs (UntappedValue (SFT_MVAL sft))
netFlowRate :: Lens' amuLs (SFT_MVAL sft)
instance MonetaryUnitLenses amuLs sft
=> Semigroup (MonetaryUnitData amuLs sft) where
(<>) (MkMonetaryUnitData a) (MkMonetaryUnitData b) =
let c = a & set settledAt ( b^.settledAt)
& over settledUntappedValue (+ b^.settledUntappedValue)
& over netFlowRate (+ b^.netFlowRate)
in MkMonetaryUnitData cinstance MonetaryUnitLenses amuLs sft
=> AgreementMonetaryUnitData (MonetaryUnitData amuLs sft) sft where
balanceProvidedByAgreement (MkMonetaryUnitData a) t = typedValuesToRTB
( UntappedValue $ uval_s + fr * fromIntegral (t - t_s) ) []
where t_s = a^.settledAt
UntappedValue uval_s = a^.settledUntappedValue
fr = a^.netFlowRate-- ... some defintions are omitted for brevity ...
applyAgreementOperation (UpdateFlow newFlowRate) acd t' = let
acd' = ContractData { flow_last_updated_at = t'
, flow_rate = newFlowRate
}
aorΔ = OperationPartiesF
(def & set CFMUD.settledAt t'
& set CFMUD.netFlowRate (-flowRateΔ)
& set CFMUD.settledUntappedValue (UntappedValue $ -settledΔ)
)
(def & set CFMUD.settledAt t'
& set CFMUD.netFlowRate flowRateΔ
& set CFMUD.settledUntappedValue (UntappedValue settledΔ)
)
in (acd', fmap CFMUD.MkMonetaryUnitData aorΔ)
where t = flow_last_updated_at acd
fr = flow_rate acd
settledΔ = fr * fromIntegral (t' - t) -- !! KEY equition
flowRateΔ = newFlowRate - frSemantic: Party A sends a flow of money at a decaying rate Λ to party B with a distribution limit of X.
- For recipient looks like receiving money over a decaying curve (with a half-life determined by Λ):

balanceProvidedByAgreement (MkMonetaryUnitData a) t = typedValuesToRTB
( UntappedValue $ ceiling $ α * exp (-λ * t_Δ) + ε ) []
where t_s = a^.settledAt
α = a^.αVal
ε = a^.εVal
λ = a^.decayingFactor
t_Δ = fromIntegral (t - t_s)- Similar to CFA it is scalable, but only for the same
Λvalue.
Challenge: How to augment previously mentioned semantics with 1 to N proportional distribution semantic?
- Lenses come to the rescue.
- Indexes are where the actual lenses are provided.
- A reminder, lenses for the
ConstantFlow:class (Default amuLs, SuperfluidTypes sft) => MonetaryUnitLenses amuLs sft | amuLs -> sft where settledAt :: Lens' amuLs (SFT_TS sft) settledUntappedValue :: Lens' amuLs (UntappedValue (SFT_MVAL sft)) netFlowRate :: Lens' amuLs (SFT_MVAL sft)

- For all (∀, universal) monetary unit data there exists one and only one set of universal lenses.
- As a result, combining
ConstantFlowand universal indexed lenses gives you the 1to1 semantic agreements:- Instant Transfer Agreement (ITA)
- Constant Flow Agreement (CFA)
- Decaying Flow Agreement (DFA)
- etc.

data UniversalData sft = UniversalData -- UniversalMonetaryUnitData
{ -- ...
, cfa_settled_at :: SFT_TS sft
-- ...
-- | Monetary unit lenses for the universal index.
instance SuperfluidTypes sft => CFMUD.MonetaryUnitLenses (UniversalData sft) sft where
settledAt = $(field 'cfa_settled_at)
settledUntappedValue = $(field 'cfa_settled_untapped_value)
netFlowRate = $(field 'cfa_net_flow_rate)- A publisher owns a distribution.
- Each distribution can have any number of subscribers.
- Each subscriber owns a number of units in the distribution.
- Subscribers can receive money distributions from the publisher proportionally per their number of units.
Constant Flow Distribution Agreement.

Sub systems created through “agreement framework” have:
- π function - providing a portion of real time balance to the monetary unit data value function, with time also part of its input.
- ω function - transforming data or create agreement monetary unit data delta monoids that affect the inputs to the π function.
-
Lens abstraction - A optional technique to compose smaller building blocks for
1to1and1toN proportional distributionsemantics.
- Instant Transfer Agreement (payment as we are familiar with)
- Constant Flow Agreement (1to1 constant money flows)
- Decaying Flow Agreement (1to1 decaying money flow with a distribution limit and a half-life of flow rate)
- Instant Distribution Agreement (1toN instant transfer)
- Constant Flow Distribution Agreement (1toN constant money flows)
How to have compositionality and add context to the system?

DISCLAIMER: Not everything mentioned here is implemented in the spec yet, but we will show the working Haskell code that demonstrates the main idea.
-- simplified for brevity
class AgreementOperationWithData a where
runAgreement :: a -> IO ()
data PaperAgreement = MkPaperAgreement String
instance AgreementOperationWithData PaperAgreement where
runAgreement (MkPaperAgreement s) = putStrLn s
-- | A contract executable within the IO monad context.
data Contract = Contract
{ contractPreCond :: IO Bool
, contractExecs :: [AnyAgreementOperationWithData]
, contractAttachedCond :: (IO Bool, AnyAgreementOperationWithData)
}
-- Define an existential type to avoid an explicit sum type...
data AnyAgreementOperationWithData = forall a.
AgreementOperationWithData a => MkAnyAOD a
instance AgreementOperationWithData AnyAgreementOperationWithData where
runAgreement (MkAnyAOD a) = runAgreement adata Contract = Contract
{ contractPreCond :: IO Bool
, contractExecs :: [AnyAgreementOperationWithData]
, contractAttachedCond :: (IO Bool, AnyAgreementOperationWithData)
}
execContract :: Contract -> IO ()
execContract (Contract preCond execs _) = do
pred <- preCond
if pred then mapM_ runAgreement execs
else putStrLn "No bueno, amigo"
execCondContract :: Contract -> IO ()
execCondContract (Contract _ _ (cond, a)) = do
pred <- cond
if pred then runAgreement a
else putStrLn "No tan rápida, amigo"main = do
brrr <- newIORef False
let sec_says_no = return False
let sec_says_yes = return True
let when_money_goes_brrr = readIORef brrr
let c0 = Contract
sec_says_no
[ MkAnyAOD $ (MkPaperAgreement "Elon Musk buys Twitter") ]
(return False, MkAnyAOD $ MkPaperAgreement "Not possible")
let c1 = Contract
sec_says_yes
[ MkAnyAOD $ MkPaperAgreement "Bob sends Alice $42 dollar"
, MkAnyAOD $ MkPaperAgreement "Alice sends Carol $4.2 dollar"
]
( when_money_goes_brrr,
MkAnyAOD $ MkPaperAgreement "Alice pays Bob back $420 dollars" )putStrLn "# Contract 0"
execContract c0
putStrLn "# Contract 1"
execContract c1
execCondContract c1
putStrLn "Money goes brrr..."
writeIORef brrr True
execCondContract c1# Contract 0
No bueno, amigo
# Contract 1
Bob sends Alice $42 dollar
Alice sends Carol $4.2 dollar
No tan rápida, amigo
Money goes brrr...
Alice pays Bob back $420 dollars
“How to write a financial contract” by Simon Peyton Jones & Microsoft Research.
European option: at a particular date you may choose to acquire an “underlying” contract, or to decline
or :: Contract -> Contract -> Contract
-- Acquire either c1 or c2 immediately
zero :: Contract
-- A worthless contract
european :: Date -> Contract -> Contract
european t u = at t (u `or` zero)Money at dynamic level has “potential to update its context”.

- Let side effects make money useful!
- We already see the toy example using IO monad, in real implementation these are needed side effects:
- Load data from storage.
- Read context such as time.
- Authentication (Blockchain digital signature).
- Authorization (Who can update whose agreement?).
- Atomic transaction, for composed contract.
- …
class ( Monad tk
, SuperfluidTypes sft
, Account acc sft
) => Token tk acc sft | tk -> acc, tk -> sft where
balanceOfAccount :: ACC_ADDR acc -> tk (SFT_RTB sft)
transfer :: CONTRACT_ACC_ADDR acc (ITA.Operation sft) -> SFT_MVAL sft -> tk ()
updateFlow :: CONTRACT_ACC_ADDR acc (CFA.Operation sft) -> CFA.FlowRate sft -> tk ()
-- ...
distributeProportionally
:: ACC_ADDR acc -- publisher
-> ProportionalDistributionIndexID -- indexId
-> SFT_MVAL sft -- amount
-> tk ()
-- ...- Token is like a bank, and it manages accounts.
- But note can be modeled similarly too as an monad!
- Choose effect systems: mtl, transformers, free monads, polysemy.
- Early Superfluid Protocol idea is implemented for EVM blockchains in Solidity language.
- Not all the denotational semantics have been implemented.
- Live in production: Polygon, Gnosis Chain, Optimism, Arbitrum, Avalanche, BSC.
- Achieved stats: >= 30K addresses, >= $10M streamed a month.
- Still work in progress, but already functional.
- Plan to fully support and prototype new denotational semantics for payment.
- Plan to also work on financial contract combinators, inspired by Simon Peyton Jones’ “Composing contracts” paper[fn:peyton2000composing].
“Here’s a categorical rule of thumb: every time you have composition, you should look for a category.”
- Bartosz Milewski

“Category theory is the study of compositionality: building big things out of little things, preserving guarantees.”
- Ken Scambler
- Victor Frankl
-
Victor Frankl/jk
- Philip Wadler


Limit / Colimit.

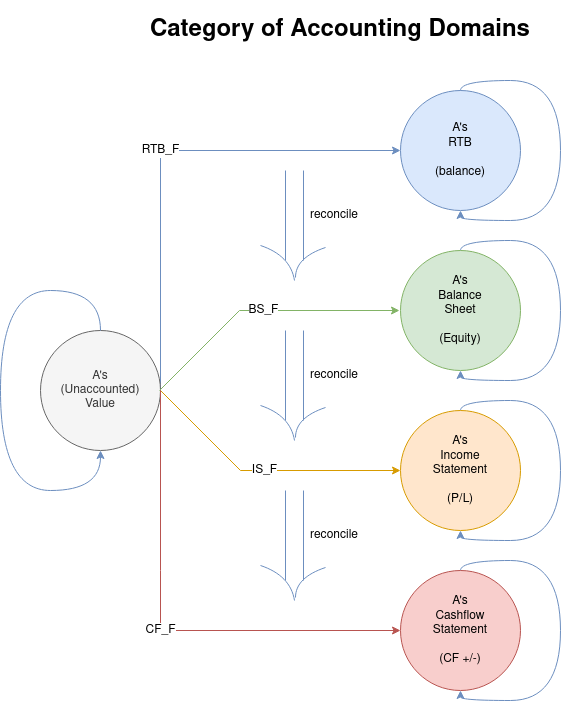
- Real Time Payment - A money distribution where the value of each monetary unit in it is also a function of time.
- Compositionaility - The morphism of the money distribution are composed financial contracts.
- Real Time Accounting - Natural transformations between different accounting domains (RTB of Account, Balance Sheet, Income Statement, Cashflow Statement, etc.)
- Superfluid monorepo: https://github.com/superfluid-finance/protocol-monorepo/
- Presentation source:
- https://raw.githubusercontent.com/wiki/superfluid-finance/protocol-monorepo/Presentation-denotational-payment/index.org
- http://raw.githack.com/wiki/superfluid-finance/protocol-monorepo/Presentation-denotational-payment/index.html
[fn:fmus] https://www.corporatetobank.com/resources/payment-clearing-and-settlement-systems/ [fn:peyton2000composing] Peyton Jones, Simon, Jean-Marc Eber, and Julian Seward. “Composing contracts: an adventure in financial engineering (functional pearl).” ACM SIGPLAN Notices 35, no. 9 (2000): 280-292.
- Governance Overview
- For Contributors
- Development Process
- Protocol EVMv1 Operations
- Protocol EVMv1 Technical Notes
- Protocol EVMv1 Core Subgraph